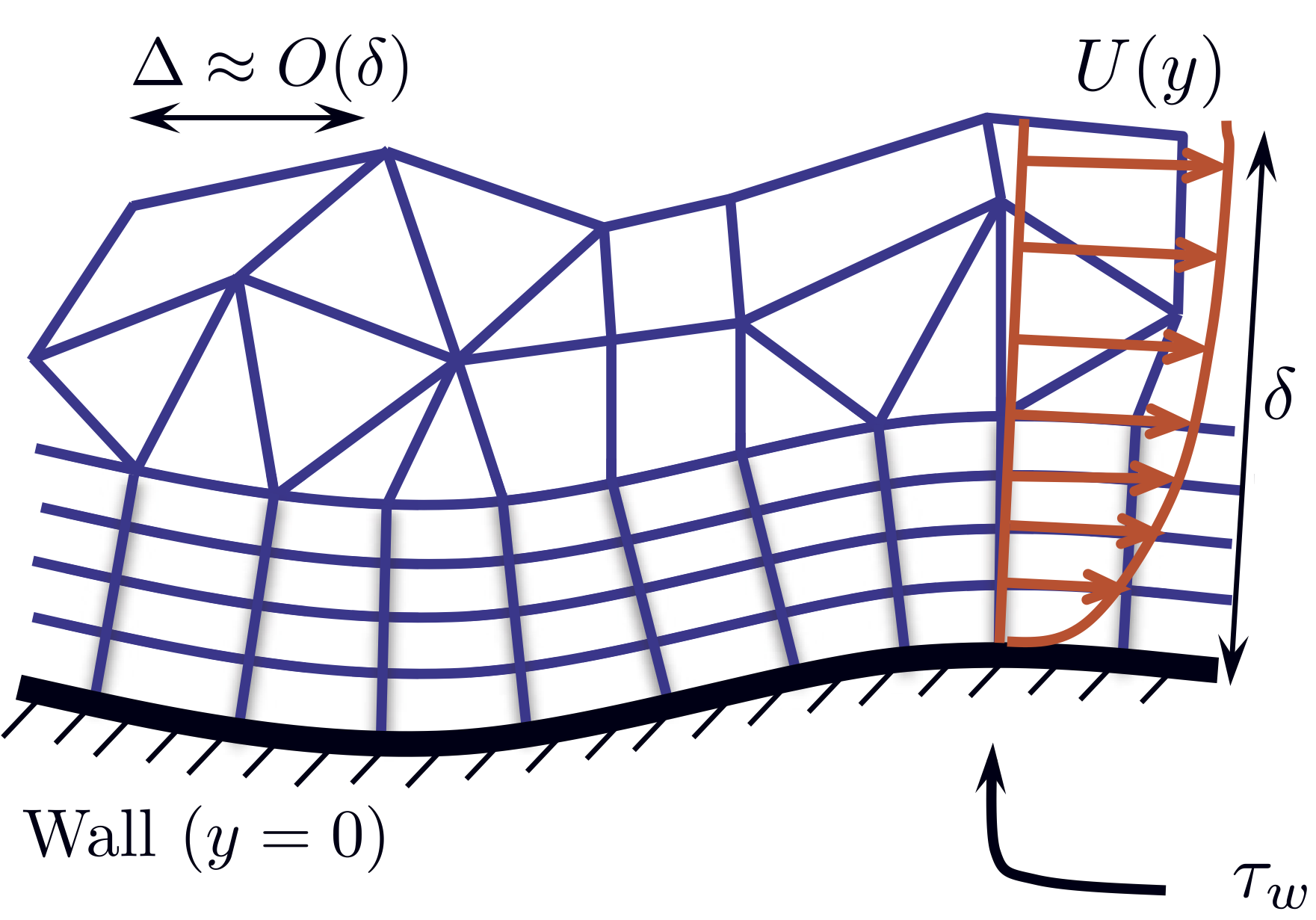
Large-Eddy Simulation (LES) with Near-Wall Modeling
Turbulence is more the rule than the exception in fluids engineering problems at the scales of our daily life. A hallmark of turbulence is the presence of wide ranges of length and time scales, the extents of which broaden with Reynolds number. High Reynolds number turbulence in itself is therefore a multi-scale phenomenon. Solid walls, which are indispensable parts in engineering applications, further limit the size of the energetic turbulent eddies to their distance from the wall. First principles based prediction of high Reynolds number wall turbulence must resolve these dynamically important eddies which get progressively smaller toward the wall. However, such direct approaches are not feasible due to the prohibitive computational cost. It is clear that a less costly approach to account for the effect of inner-layer dynamics is needed.
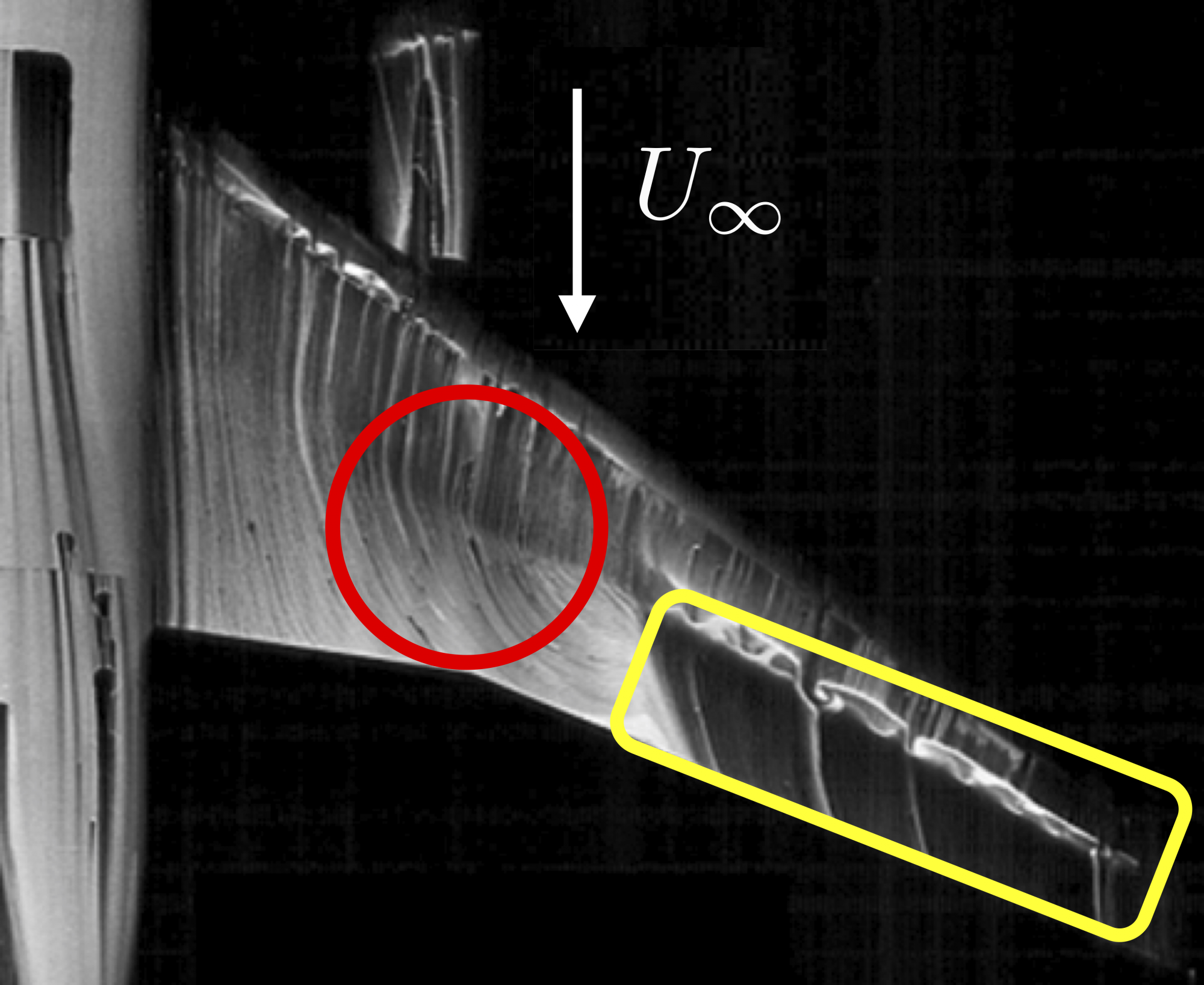
Nonequilibrium Turbulent Boundary Layers
The vast knowledge of equilibrium turbulence in channel, pipe, and flat plate gained over the last 50 years has had limited impact on our ability to predict practical flows of interest, because turbulent boundary layers in realistic flows are affected strongly by nonequilibrium effects controlled by flow-dependent boundary conditions. Consequently, the law-of-the-wall, scaling laws, and reduced-order models established largely for equilibrium turbulent boundary layer cannot be generalized to non-canonical flows. Additionally, rapid variations in strain and vorticity often present in such flows render many turbulence closure models calibrated to equilibrium turbulence of limited utility. Examples of such nonequilibrium flows with particular relevance to external aerodynamics and ship hydrodynamics are turbulent boundary layer with mean-flow three dimensionality and/or pressure gradients.

Fluid-Structure Interaction (FSI): Numerical Method & Modeling
In mathematical description of wall-bounded flows, solid geometries enter the equation of fluid motions often only through the locations where kinematic boundary conditions are imposed. However, richer physical descriptions are called for when the solid body has its own dynamics, undergoes finite deformation in response to the flow, and conducts heat internally. A central research challenge is the development of unified computational framework for multi-material simulation which can robustly handle moving/deforming geometries without sacrificing accuracy and physical consistency. To this end, exploring numerical methods which satisfy conservation principles of the primary (mass, momentum) and secondary quantities (energy, entropy), both locally and globally, is of great importance.